Моделирование эталонных отражателей, используемых при построении радиолокационного изображения спутников
Известны различные варианты отражателей [3, 4], предназначенных для калибровки радиолокационных станций, например металлические сферы или уголковые отражатели. Металлические сферы являются удобными эталонными рассеивателями, эффективную площадь рассеивания (ЭПР) которых можно точно вычислить. В силу симметрии рассеяния ЭПР у сферы постоянна и не зависит от длины волны излучаемой РЛС (при условии, что радиус сферы больше длины волны). Недостатком сферического отражателя является малая ЭПР. Именно поэтому в качестве калибровочных отражателей чаще используются трехгранные уголковые отражатели, имеющие по сравнению со сферическими отражателями существенно большую ЭПР. Радиолокационный уголковый отражатель состоит из трех взаимно перпендикулярных металлических плоскостей обычно прямоугольной или треугольной формы. Луч, падающий на одну из плоскостей под малым углом относительно биссектрисы трехгранного угла, после трехкратного отражения возвращается в направлении источника излучения. Максимальное значение достигается при совпадении падающего луча с биссектрисой трехгранного угла.
Для радиолокационного уголкового отражателя с квадратными гранями ЭПР рассчитывается по формуле:
Для радиолокационного уголкового отражателя с треугольными гранями ЭПР рассчитывается по формуле:
В этих выражениях σ — значение ЭПР, a — сторона квадрата или катет треугольника, λ — длина волны.
Для исследования основных параметров указанных выше устройств и получения отражательных характеристик был проведен анализ существующих программных продуктов (Mathcad, Maple), позволяющих реализовать математические модели устройств. Анализ показал, что среда графического программирования LabVIEW позволяет создать виртуальный прибор, с помощью которого можно исследовать форму и основные параметры отраженного сигнала [1–4].
Для наглядности сравниваются эффективные площади рассеяния радиолокационного уголкового отражателя с квадратными гранями и радиолокационного уголкового отражателя с треугольными гранями.
Созданный виртуальный прибор (рис. 1) в среде LabVIEW позволяет задать необходимую длину волны, излучаемую РЛС [5, 6], а также ввести расчетные размеры радиолокационных уголковых отражателей с квадратными и треугольными гранями.
Эти параметры вводятся на лицевой панели виртуального прибора (рис. 2).
Изменяя длину волны РЛС или длину грани радиолокационного уголкового отражателя, можно построить график, который наглядно отображает полученный радиолокационный сигнал.
Описание работы виртуального прибора
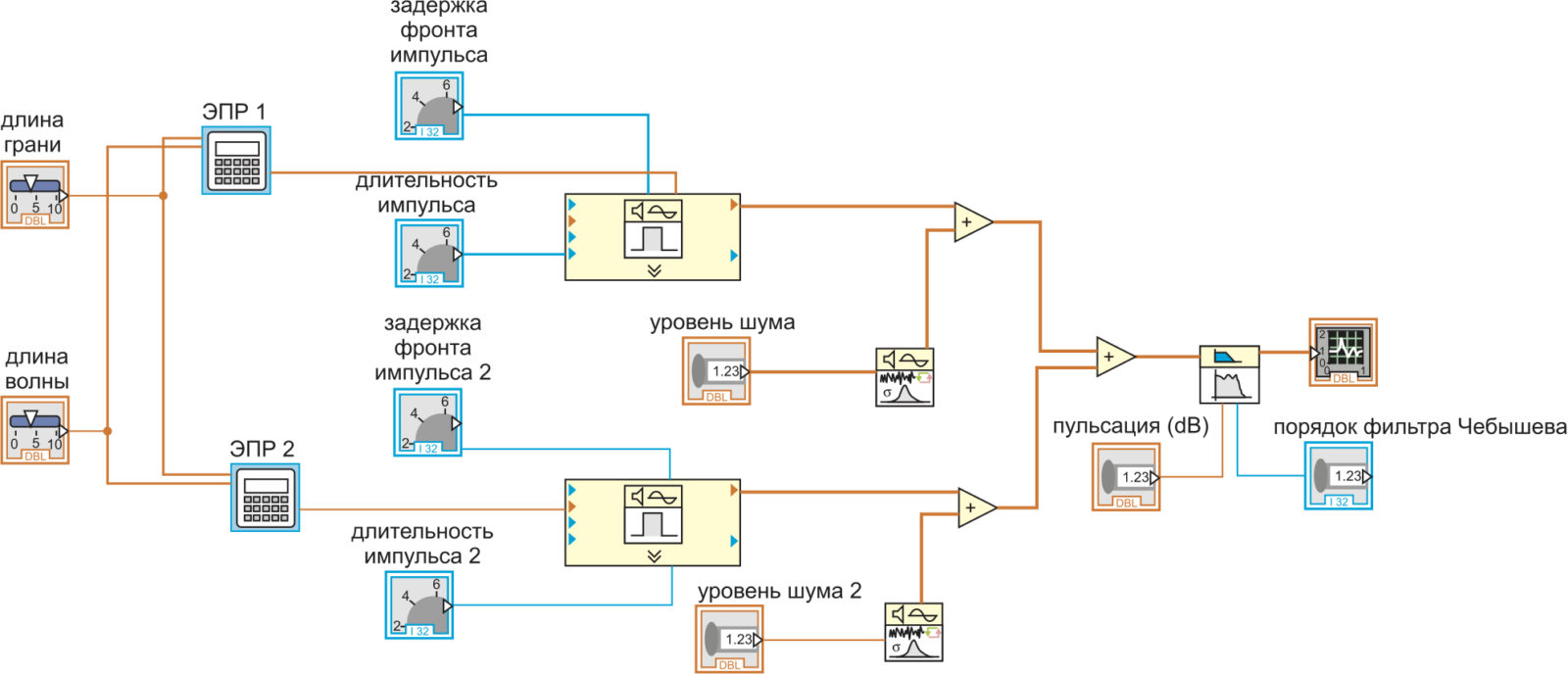
Схема виртуального прибора позволяет получить радиолокационный сигнал, отраженный от уголковых отражателей разного типа (рис. 3). В математический блок введены формулы, необходимые для расчета ЭПР соответствующих уголковых отражателей.
Пользователю необходимо указать длину грани уголкового отражателя, задать длину волны и длительность импульса. Оба уголковых отражателя облучаются одной волной. Имеется возможность разнести полученные сигналы по времени путем задержки фронта импульса. При вводе необходимых параметров, на лицевой панели виртуального прибора отображается зависимость ЭПР от параметров сигнала.
Таким образом, созданный виртуальный прибор позволяет осуществлять моделирование ЭПР для радиолокационных уголковых отражателей с квадратными и треугольными гранями.
- Трэвис Дж., Кринг Дж. LabVIEW для всех. М.: ДМК-Пресс, 2011.
- Кетарнаваз Н., Ким Н. Цифровая обработка сигналов на системном уровне с использованием LabVIEW. М.: ДоДека-ХХI, 2007.
- Кобак В. О., Радиолокационные отражатели. М.: «Сов. радио», 1975.
- Сколник М. И., Справочник по радиолокации. Пер. с англ. Под общей ред. В. С. Вербы. Книга 1. М.: Техносфера, 2014.
- Ширман Я. Д., Теоретические основы радиолокации. М.: Норма, 2012.
- Лиференко В. Д., Сидоров В. А., Королёв В. О. Компьютерное моделирование радиоэлектронной обстановки для двух типов РЛС в среде LabVIEW//Компоненты и технологии. 2016. № 10.





 8 февраля, 2021
8 февраля, 2021 26 августа, 2020
26 августа, 2020 8 декабря, 2022
8 декабря, 2022